Geo Hashing

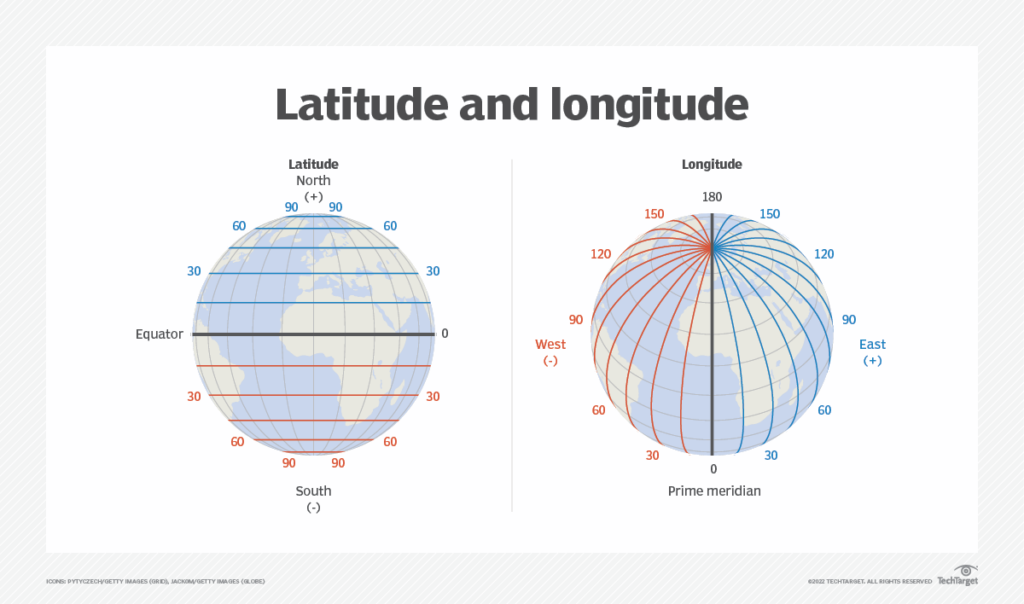
We all have studied about latitudes and longitudes in our geography classes and know that together they can be used to uniquely identify any location on the surface of earth.

But using these to store locations in a database can be a little tricky to work with becuase:

1. Float / Double representation is a pain deal with
2. Finding locations that are within certain radius of each other is costly

Lets take a simple example of a database schema storing locations of businesses :

CREATE TABLE business_locations (
    business_id int,
    latitude float,
    longitude float,
    name varchar,
    category varchar
);

Given the location of a user who wants to find all businesses near him within a radius r, we would query it as follows

SELECT * FROM business_locations 
WHERE latitude BETWEEN user_lat - r AND user_lat + r
AND longitude BETWEEN user_lng - r AND user_lng + r

Even if we add an index on latitude and longitude, we wont be able to solve the problem efficiently because :

1. After using the index on latitude for range query, any other index columns are not used
2. Even if it was being used then also intersecting these two huge lists in memory is very bad design

To solve this problem efficiently and at scale one of the most commonly used solutions is GeoHashing.

Geohash is a public domain geocode system invented in 2008 by Gustavo Niemeyer.

The idea is simple but very powerful. We are going to divide the world in grids, and number each grid.

Then for each subgrid we are again going to divide it into grids and number it again the same way.

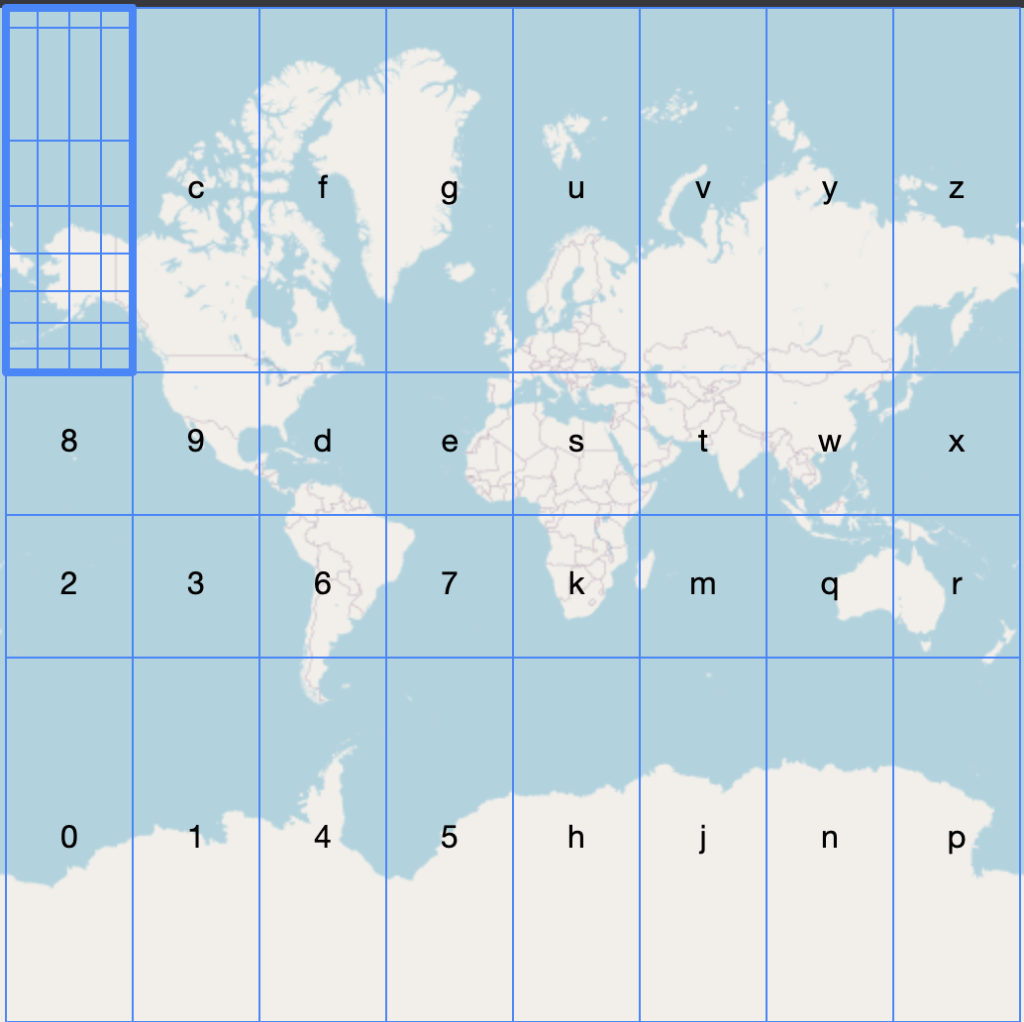
The more we are going to subdivide each grid the smaller the area becomes and more precision we get for each character that we add.

geohash length	km error
1	±2,500 km (1,600 mi)
2	±630 km (390 mi)
3	±78 km (48 mi)
4	±20 km (12 mi)
5	±2.4 km (1.5 mi; 2,400 m)
6	±0.61 km (0.38 mi; 610 m)
7	±0.076 km (0.047 mi; 76 m)
8	±0.019 km (0.012 mi; 19 m)

The problem with our previous SQL query is that we are trying to search in a 2D space using a model which is best suited for answering 1D queries. So we need some way to convert this information of (latitude, longitude) pair into a single value.

This problem has been studied for decades, and there are many types of curves that can be used to this for us. Its called the space filling curve. Some examples include:

1. Hilbert curve
2. Z curve (This is whats used in standard GeoHashing)
3. S-Curve (Google uses this for their GeoHashing use case)

Latitude / Longitude to GeoHash

That being said how do we convert between our old latitude, longitude values and this new shiny GeoHash.

Remember that latitudes have values between [-90, 90] and longitudes have the range [-180, 180]

Lets take an example of (19.3, 20.5)

We first have to convert this lat-long pair into a binary representation, but we are not going to use IEEE format for doing so, because ???

We are going to start with our initial range [-90, 90] and our target 19.3 and start splitting the current range and add a 1-bit when our target belongs to left range or 0 if it belongs to right.

1. [-90, 90] after split [-90, 0) [0, 90], our target 19.3 belongs to right range.
2. [0, 90] after split [0, 45) [45, 90], our target 19.3 belongs to left range.
3. [0, 45) after split [0, 22.5) [22.5, 45], our target 19.3 belongs to left range.
4. [0, 22.5) after split [0, 11.25) [11.25, 22.5], our target 19.3 belongs to right range.
5. …. and so on

So our final latitude in binary will be something like 1001…

We can go on until we have a good enough estimation of the latitude in our binary format, until 32 bits.

We do the same thing with longitude also, but the starting range is [-180, 180].

Once we have the binary lat-long values we are now going to interleave both these binary values to get a single 64 bit long value.

Say our lat binary value was 101111001001 and long binary value was 0111110000000

Then after interleaving we will have (01101 11111 11000 00100 00010)

After generating this 64 bit value we are going to split it into 5-bit pieces and convert it into a base 32 format using the below table.

Decimal	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Base 32	0	1	2	3	4	5	6	7	8	9	b	c	d	e	f	g
Decimal	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
Base 32	h	j	k	m	n	p	q	r	s	t	u	v	w	x	y	z

The final reduced geo hash we get is ezs42

Visualizing this geo hash in terms of the world map is also very intuitive. Start from left the first char is e, which means we select the e box in our grid. Then we subdivide the selected grid box and then choose the z box in our grid ….

Advantages of using GeoHash:

1. Given two geohashes by simply matching their prefix we can tell how close together they are.
2. Easy to store as string in our databases.

Edge cases:

While comparing two geohashes looks very easy on surface there are two caveats to take care of while working with them

1. Sometimes two locations can be very close to each other and have 0 prefix overlap. This occurs because we have strict definitions of our grids. So two locations on either side of prime meridian will have 0 overlaps even if they are few kms apart.
2. Since a geohash (in this implementation) is based on coordinates of longitude and latitude the distance between two geohashes reflects the distance in latitude/longitude coordinates between two points, which does not translate to actual distance.

We can solve the edge cases problem by first finding all the nearby geohashes of the code we are looking for and searching those too in our query to be 100 percent sure that all cases are covered.